正定矩阵
Contents
正定矩阵#
定义#
令 \(\pmb{A}\) 为一个 \(n\times n\) 实对称矩阵,当且仅当对所有 \(n\) 维非零向量 \(\pmb{x}\) ,都有:
则称 \(\pmb{A}\) 为正定(positive definite);若上述条件为:
则称 \(\pmb{A}\) 为半正定(positive semidefinite).
分析#
在上述关于正定矩阵的定义中,之所以强调 \(\pmb{A}\) 是实对称矩阵,是因为任何一个实数方阵,都可以表示为一个实对称矩阵与一个反对称矩阵的和,即 \(\pmb{A}=\pmb{B}+\pmb{C}\) (称为卡氏分解),其中:
计算可验证:\(\pmb{B}=\pmb{B}^{\rm{T}}\) 、\(\pmb{C}=-\pmb{C}^{\rm{T}}\) 。所以,\(\pmb{B}\) 是对称矩阵,\(\pmb{C}\) 是反对称矩阵(反对称矩阵,也称为“斜对称矩阵”\(^{[2]}\))。
考虑:
因为:
故 \(\pmb{x}^{\rm{T}}\pmb{Cx} = 0\) ,因此
即二次型 \(\pmb{x}^{\rm{T}}\pmb{Ax}\) 可用对称部分表示。
几何意义#
若 \(n=1\) ,则矩阵 \(\pmb{A}\) 和向量 \(\pmb{x}\) 都退化为标量 \(a、x\) ,对任意非零的 \(x\) ,有:\(xax=ax^2\gt0\) 。
显然 \(a\) 是正数,完整地说,\(a\) 是正定的。
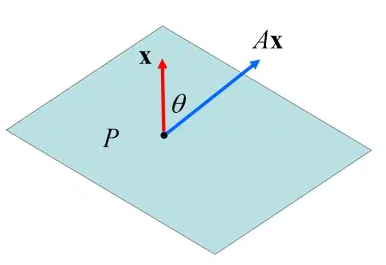
若 \(n\gt1\) ,\(\pmb{Ax}\) 与 \(\pmb{x}\) 之间的夹角 \(\theta\) 的余弦为 \(\cos\theta = \frac{\pmb{x}^{\rm{T}}(\pmb{Ax})}{\begin{Vmatrix}\pmb{x}\end{Vmatrix}\begin{Vmatrix}\pmb{Ax}\end{Vmatrix}}\) 。
\(\pmb{Ax}\) 与 \(\pmb{x}\) 点积为正值,则 \(\theta \lt 90°\) ,如下图所示,\(\pmb{x}\) 为超平面 \(P\) 的法向量,正定矩阵 \(\pmb{A}\) 保证变换后的向量 \(\pmb{Ax}\) 与原向量 \(\pmb{x}\) 都位于超平面 \(P\) 的同一侧。
对称正定矩阵的对角化形式 \(\pmb{A}=\pmb{Q\Lambda Q}^{\rm{-1}}\) 的几何解释:
\(\pmb{A}\sim\pmb{\Lambda}\) ,\(\pmb{A}\) 参考有序基 \(\{\pmb{q}_1,\cdots,\pmb{q}_n\}\) 的变换矩阵即为对角矩阵 \(\pmb{\Lambda}\) 。由于每个主对角元素都大于零,对称正定矩阵具有分别拉伸各主轴(即特征向量方向)的功能,而伸缩量即为特征值。
还可以认为连续执行了三个线性变换:
\(\pmb{Q}^{-1}\) :旋转变换
\(\pmb{\Lambda}\):拉伸变换
\(\pmb{Q}\) :逆旋转变换
定理#
若 \(\pmb{A}\) 是一个实对称正定矩阵,则 \(\pmb{A}\) 的特征值皆为正,反之亦然。
证明
(1)\(\pmb{A}\) 是实对称正定矩阵,令 \(\pmb{A}=\pmb{Q\Lambda Q}^{\rm{T}}\) ,其中 \(\pmb{\Lambda} = \rm{diag}(\lambda_1,\cdots,\lambda_n)\) ,\(\lambda_i\) 是 \(\pmb{A}\) 的特征值。
设 \(\pmb{Q}=\begin{bmatrix}\pmb{q}_1&\cdots&\pmb{q}_n\end{bmatrix}\) 的所有列都是单范正交特征向量。
因为 \(\pmb{A}\) 正定,所以:
(2)设 \(\lambda_i\gt0,(i=1,\cdots,n)\) 。令 \(\pmb{y}=\pmb{Q}^{\rm{T}}\pmb{x}=\pmb{Q}^{-1}\pmb{x}\) 。因为 \(\pmb{x} = \pmb{Qy}\) ,\(\pmb{y}\) 必定为非零向量,则:
性质#
性质1:正定矩阵的每一个主子阵都是正定的
证明
为了证明此性质,首先引入一种符号记法。
令 \(S\) 为 \(\{1,2,\cdots,n \}\) 的子集,\(S^{\rm{c}}\) 表示 \(S\) 的补集,\(|S|\) 表示集合 \(S\) 的元素数,称为基数(cardinal number)。对于所有 \(i\in S^{\rm{c}}\) ,将 \(n\times n\) 阶矩阵 \(\pmb{A}\) 的第 \(i\) 行与第 \(i\) 列同时删除,可得到一个 \(|S|\times |S|\) 阶主子阵(principal submatrix),以 \(\pmb{A}_S\) 表示。例如:
下面几个都是主子阵:
对于向量 \(\pmb{x}\in\mathbb{R}^n\) ,用 \(\pmb{x}_{S}\) 表示删除了 \(S\) 的补集元素后得到的向量,显然 \(\pmb{x}_S\) 是 \(|S|\) 维向量。
对于任何 \(k\in S^{\rm{c}}\) ,令 \(\pmb{x}\) 的第 \(k\) 个元为零,则:
由于 \(\pmb{x}_S\ne0\) 是任意的,所以 \(\pmb{A}_S\) 是正定的。
性质2:正定矩阵的特征值皆为正数
证明
设 \(\lambda\) 为正定矩阵 \(\pmb{A}\) 的一个特征值,对于特征向量 \(\pmb{x}\ne0\) ,则:
则:\(\lambda=\frac{\pmb{x}^{\rm{T}}\pmb{Ax}}{\pmb{x}^{\rm{T}}\pmb{x}}\) ,分子分母都是正数,故 \(\lambda\gt0\) 。
拓展
由性质2可知:设 \(\lambda_i\gt0\) 是正定矩阵 \(\pmb{A}\) 的特征值,则 \(\pmb{A}\) 可逆, \(\pmb{A}^{-1}\) 和 \(\pmb{A}^{\rm{T}}\) 也是正定矩阵,且:
结合性质1,每个主子阵 \(\pmb{A}_S\) 亦有类似性质。
性质3:正定矩阵的主元(pivot)都是正数
性质4:正定矩阵 \(\pmb{A}\) 可以表示为 \(\pmb{A}=\pmb{B}^{\rm{T}}\pmb{B}\) ,\(\pmb{B}\) 是一个可逆矩阵
判别#
若 \(n\times n\) 矩阵 \(\pmb{A}\) 的特征值都是正数,则 \(\pmb{A}\) 是正定矩阵
若 \(n\times n\) 矩阵 \(\pmb{A}\) 的轴(主元)都是正数,则 \(\pmb{A}\) 是正定矩阵
若 \(n\times n\) 矩阵 \(\pmb{A}\) 的领先主子阵的行列式都是正数,则 \(\pmb{A}\) 是正定矩阵
若 \(n\times n\) 矩阵 \(\pmb{A}\) 可表示为 \(\pmb{A}=\pmb{B}^{\rm{T}}\pmb{B}\) ,\(\pmb{B}\) 是一个可逆矩阵,则 \(\pmb{A}\) 是正定矩阵
参考文献#
[1]. 特殊矩阵-六:正定矩阵
[2]. 反对称矩阵:指满足 \(\pmb{A}^{\text{T}}=-\pmb{A}\) 的矩阵,或者,对于矩阵 \(\pmb{A}=(a_{ij})\) ,各元素的关系为 \(a_{ij}=-a{ji}\) ,例如下面的矩阵就是一个反对称矩阵:
反对称矩阵特性:
反对称矩阵自身相乘的积是对称矩阵
对任意矩阵 \(\pmb{A}\) ,\(\pmb{A}^{\text{T}}-\pmb{A}\) 是反对称矩阵
若 \(\pmb{A}\) 是反对称矩阵,\(\pmb{x}\) 是向量,则 \(\pmb{x}^{\text{T}}\pmb{Ax}=0\)
反对称矩阵的主对角线匀速必是零,所以其迹为零
