费雪的线性判别分析
Contents
费雪的线性判别分析#
本文可作为《机器学习数学基础》\(^{[2]}\)的 285 页(0-1)分布相关内容的拓展阅读。
1. 缘起#
对于线性判别分析的介绍,在网上或者有关书籍中,均能找到不少资料。但是,诸多内容中,未能给予线性判别分析完整地讲解,本文不揣冒昧,斗胆对其中的一部分内容,即费雪的线性判别分析进行整理,权当自己的学习笔记,在这里发布出来,供朋友们参考。
2. 费雪的线性判别分析#
英国统计学家费雪(Ronald Fisher)提出的专门针对含有两个类别样本的有监督的降维方法,称为“费雪的线性判别分析(Fisher Linear Discriminant Analysis)。
费雪的线性判别分析基本思想是(如图1所示):
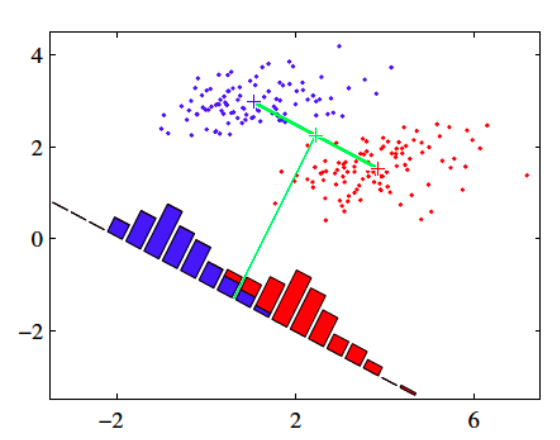
图 1
获得数据在某直线(超平面)上的投影,并同时要求:
类内散度最小
类间散度最大
多数资料中介绍线性判别分析的时候,都是按照上述费雪所提出的线性判别分析思想讲解的。
本文也首先介绍上述基本思想,而后引申出其他相关问题。
2.1 二分类的样本数据#
设数据样本 \(\{\pmb{x}_1,\cdots,\pmb{x}_n\}\in\mathbb{R}^d\) ,样本数量大小为 \(n\) ,特征数(维数)是 \(d\) 。
假设此样本分为两类,类别 \(C_1\) ,样本数量为 \(n_1\) ;类别 \(C_2\) ,样本数量为 \(n_2\) 。并且 \(n=n_1+n_2\) 。
2.2 问题:投影可能重叠#
设有一条直线 L ,用单位向量 \(\pmb{w}\) (\(\begin{Vmatrix}\pmb{w}\end{Vmatrix}^2=\pmb{w}^{\text{T}}\pmb{w}=1\))表示此直线的方向。
若将样本中的任意一个向量 \(\pmb{x}\) 向此直线投影,得到投影量 \(y\pmb{w}\) ,其中 \(y\) 表示投影的大小(长度)。
由于 \(\pmb{x}-y\pmb{w}\) 与单位向量 \(\pmb{w}\) 正交,即:\(\pmb{w}^{\text{T}}(\pmb{x}-y\pmb{w})=0\) ,所以:
故样本中每个样本 \(\pmb{x}_1,\cdots,\pmb{x}_n\) 在直线 L 上的投影大小 \(y_1,\cdots,y_n\) 为:
将 \(\pmb{x}_1,\cdots,\pmb{x}_n\) 所在的空间称为 \(X\) 空间,投影 \(y_1,\cdots,y_n\) 所在的空间称为 \(Y\) 空间。
根据(2)式结果,可以得到 \(Y\) 空间的每个类别样本的投影大小的平均数:
令 \(\pmb{m}_j=\frac{1}{n_j}\sum\limits_{i\in C_j}\pmb{x}_i\) (\(j=1,2\)),代表 \(X\) 空间的某个类别的所有样本的平均数向量(样本平均),故(3)式可以继续表示为:
由于可以用均值表示数据的集中趋势\(^{[2]}\) ,那么向量 \(\pmb{m}_j\) ,就可以作为对应类别的中心的度量。则(4)式即表示将 \(X\) 空间的每个类别的样本平均(即该类别的中心,或称“类别中心”)投影到直线 L ,得到了 \(Y\) 空间上每个类别样本投影的平均数(即 \(\hat{m}_j\) ,表示该类别样本投影的中心,或称“类别投影中心”)。
于是得到两个类别投影中心的距离:
(5)式说明,类别投影中心的距离( \(|\hat{m}_2-\hat{m}_1|\) )等于类别中心的距离(即 \(|\pmb{m}_2-\pmb{m}_1|\))的投影 \(|\pmb{w}^{\text{T}}(\pmb{m}_2-\pmb{m}_1)|\) 。
数据点与数据点之间的距离,表征了数据的分散程度,统计学中使用方差衡量数据的分散程度 (样本方差: \(s^2=\frac{1}{n-1}\sum\limits_{i=1}^n(x_i-\overline{x})^2\) )\(^{[2]}\) 。因此,可以使用 \((\hat{m}_2-\hat{m}_1)^2\) 度量不同类别投影中心的分散程度,并将其命名为类间散度(Between-class scatter),即:
散度与方差有相同的地方,都表示了数据相对平均值的分散程度。图 2 左边表示了散度较大,右边较小。

图 2
根据前述费雪的线性判别基本思想,要找到一条适合的直线,用作样本数据投影,并且要能够满足类间散度最大 ,即找到适合的 \(\pmb{w}\) ,使得 \(\left(\pmb{w}^{\text{T}}(\pmb{m}_2-\pmb{m}_1)\right)^2\) 最大化。
下面使用拉格朗日乘数法 \(^{[3]}\) 解决这个问题,但是,做一下转化,将“最大化”转化为“最小化”,在最大化的表达式前面添加一个负号。
定义拉格朗日函数:
其中 \(\lambda\) 是拉格朗日乘数。为了计算极值,必须要计算 \(\frac{\partial L}{\partial\pmb{w}}\) :
要实现(7)是中第一个式子的最小化,须令 \(\frac{\partial L}{\partial\pmb{w}}=0\) ,则:
因为 \(\frac{1}{\lambda}(\pmb{m}_2-\pmb{m}_1)^{\text{T}}\pmb{w}\) 是数量(标量),所以:
这说明直线 L 的方向与两个类别中心的距离矢量方向平行。
但是,如果按照(11)式的方式确定直线 L 方向,样本的投影有可能出现图 1 所示的重叠现象。
从降维的角度看,假设是将高维数据降到一维,图 1 演示的降维效果并不会有利于后续分类过程。
对此,费雪提出,应该兼顾类别之间和同一类别之内的样本投影的方差:
不同类别之间的样本投影的方差越大越好(如以上说明)
同一类之内的样本投影的方差越小越好
这样,在直线(或超平面)上的投影,不同的类别投影中心的距离就尽可能大;同一类别之内的样本的投影尽可能聚集在一起。
2.3 费雪准则#
前面已经确定,可以用类别的样本数据的平均数表示每个类别的样本数据的中心(即类别中心):
以下将 \(\pmb{m}_j\) 表述为每个类别分别在 \(X\) 空间的平均数向量。
在直线 L 上,类别样本数据中心的投影用样本投影的平均数表示:
以下用 \(\hat{m}_j\) 表示在 \(Y\) 空间的样本投影的平均数,即样本数据中心的投影,或称“类别投影中心”。
仿照方差的定义形式,定义 \(Y\) 空间衡量类别内数据投影相对本类别投影中心的分散程度的量:\(Y\) 空间类内散度(Within-calss scatter):
前述(6)式定义了 \(Y\) 空间的类间散度:
根据费雪的思想,既要实现 \(Y\) 空间的类间散度最大化,同时又要实现 \(Y\) 空间的类内散度最小化。也就是实现下述函数最大化:
2.4 散度矩阵#
以下分别写出 \(X\) 空间的类内、类间散度的矩阵表示形式,分别称为散度矩阵:
\(X\) 空间的每个类的类内散度矩阵:
\[ \pmb{S}_j=\sum_{i\in C_j}(\pmb{x}_i-\pmb{m}_j)(\pmb{x}_i-\pmb{m}_j)^\text{T},\quad(j=1,2)\tag{17} \]\(X\) 空间整体的类内散度矩阵:
\[ \pmb{S}_W=\pmb{S}_1+\pmb{S}_2\tag{18} \]\(X\) 空间的类间散度矩阵:
\[ \pmb{S}_B=(\pmb{m}_2-\pmb{m}_1)(\pmb{m}_2-\pmb{m}_1)^\text{T}\tag{19} \]其中 \(\pmb{m}_{j},(j=1,2)\) 见(12)式。
\(Y\) 空间的类内散度:
根据(14)式和(2)、(13)式,\(Y\) 空间的类内散度 \(\hat{s}^2_j\) 等于:
\[\begin{split} \begin{split} \hat{s}_j^2 &= \sum_{i\in C_k}(y_i-\hat{m}_j)^2,\quad(j=1,2) \\ &=\sum_{i\in C_j}(\pmb{w}^\text{T}\pmb{x}_i-\pmb{w}^\text{T}\pmb{m}_j)^2\quad(将(2)(13)式代入) \\ &=\sum_{i\in C_k}\pmb{w}^\text{T}(\pmb{x}_i-\pmb{m}_j)(\pmb{x}_i-\pmb{m}_j)^\text{T}\pmb{w} \\ &=\pmb{w}^\text{T}\left(\sum_{i\in C_k}(\pmb{x}_i-\pmb{m}_j)(\pmb{x}_i-\pmb{m}_j)^\text{T}\right)\pmb{w}\quad(将(17)式代入,得到下步结果) \\ &=\pmb{w}^\text{T}\pmb{S}_j\pmb{w} \end{split}\qquad\qquad(20) \end{split}\]故:
\[ \hat{s}_1^2+\hat{s}_2^2=\pmb{w}^\text{T}\pmb{S}_1\pmb{w}+\pmb{w}^\text{T}\pmb{S}_2\pmb{w}=\pmb{w}^\text{T}\pmb{S}_W\pmb{w}\tag{21} \]\(Y\) 空间的类间散度: \(Y\) 空间的类间散度 \((\hat{m}_2-\hat{m}_1)^2\) 等于:
\[\begin{split} \begin{split} (\hat{m}_2-\hat{m}_1)^2&=(\pmb{w}^{\text{T}}\pmb{m}_2-\pmb{w}^{\text{T}}\pmb{m}_1)^2\quad(根据(13)式) \\ &=\pmb{w}^{\text{T}}(\pmb{m}_2-\pmb{m}_1)(\pmb{m}_2-\pmb{m}_1)^\text{T}\pmb{w} \\ &=\pmb{w}^{\text{T}}\pmb{S}_B\pmb{w}\quad(将(19)式代入后) \end{split}\qquad\qquad(22) \end{split}\]于是,(16)式的费雪准则,可以用(21)式和(22)式的结果表示为:
\[ J(\pmb{w})=\frac{\pmb{w}^\text{T}\pmb{S}_B\pmb{w}}{\pmb{w}^\text{T}\pmb{S}_W\pmb{w}}\tag{23} \]由(17)和(18)式可知,\(\pmb{S}_W\) 是半正定矩阵,如果样本大小 \(n\) 大于维数 \(d\) (这种情况比较常见),则 \(\pmb{S}_W\) 一般为正定,且可逆。
由(19)式可知,\(\pmb{S}_B\) 是半正定矩阵,若 \(\pmb{m}_2\ne\pmb{m}_1\) ,则 \(\text{rank}\pmb{S}_B=1\) 。
2.5 最优化问题求解#
对(23)式的最大化求解,可以有多种方法:
法1:直接计算 \(\frac{\partial J}{\partial\pmb{w}}=0\) 求解
法2:用线性代数方法:因为(23)式也称为广义瑞利商,故可以根据冠以特征值求解
法3:拉格朗日乘数法:参考资料 [1] 中使用的这个方法,但推导过程不详细。
法1:
最直接的思路:
所以,得到(以下使用了矩阵导数,请见参考资料 [2] ):
上式两侧同时除以 \(\pmb{w}^\text{T}\pmb{S}_W\pmb{w}\) ,得:
对(26)式最后结果等号两边同时左乘 \(\pmb{S}^{-1}_W\) (其中 \(J\) 是数量(标量)函数,见(23)式),得:
又因为上式中的 \((\pmb{m}_2-\pmb{m}_1)^\text{T}\pmb{w}\) 是数量(标量),故令:\(c=(\pmb{m}_2-\pmb{m}_1)^\text{T}\pmb{w}\) ,则(27)式进一步写成:
由此,可知:直线 L 的方向 \(\pmb{w}\) 满足:
此时能够实现费雪准则的要求,即 \(J(\pmb{w})\) 最大化。
这样,就找到了最佳投影的直线(或超平面),从而实现了最佳降维的目的。
法2\(^{[6]}\):
由(18)和(19)式可知,\(\pmb{S}_B^\text{T}=\pmb{S}_B\) 、\(\pmb{S}_W^\text{T}=\pmb{S}_W\) ,即 \(\pmb{S}_B\) 和 \(\pmb{S}_W\) 都是实对称矩阵,亦即厄米矩阵,故(23)式可以看做广义瑞利商\(^{[4]}\) 。
从而对 \(J(\pmb{w})\) 的最大化问题,等价于广义特征值问题\(^{[4]}\),如下述方程:
因为 \(\pmb{S}_W\) 可逆,故:
又因为 \(\pmb{S}_W^{-1}\) 和 \(\pmb{S}_B\) 都是半正定矩阵,所以 \(\pmb{S}_W^{-1}\pmb{S}_B\) 的特征值 \(\lambda\) 是非负数,则特征向量 \(\pmb{w}\) 是实特征向量。
于是,可以对(30)式等号两边同时左乘 \(\pmb{w}^\text{T}\) ,得:
将(32)式代入到(23)式,可得:
由此可知,只要找出最大的特征值,即可得到 \(J(\pmb{w})\) 的最大值。
又因为 \(\text{rank}(\pmb{S}_W^{-1}\pmb{S}_B)=\text{rank}\pmb{S}_B=1\) ,则说明(31)式中的 \(\pmb{S}_W^{-1}\pmb{S}_B\)只有一个大于零的特征值。
将(19)式中的 \(\pmb{S}_B\) 代入到(31)式中,得:
上式中的 \((\pmb{m}_2-\pmb{m}_1)^\text{T}\pmb{w}\) 是数量(标量),故令:\(c=(\pmb{m}_2-\pmb{m}_1)^\text{T}\pmb{w}\) ,则上式进一步写成:
从而得到与(29)式同样的结论和解释。
法3:
对于(23)式,因为分子分母都有 \(\pmb{w}\) ,故 \(J(\pmb{w})\) 与 \(\pmb{w}\) 的长度无关,可以设 \(\pmb{w}^\text{T}\pmb{S}_W\pmb{w}=1\) ,则对(23)式的最大化问题,即转化为\(^{[1]}\):
根据拉格朗日乘数法\(^{[5]}\):
计算 \(\frac{\partial L}{\partial\pmb{w}}\) :
令:\(\frac{\partial L}{\partial\pmb{w}}=0\) ,则:
因为 \(\pmb{S}_W\) 可逆,所以有:\(\pmb{S}_W^{-1}\pmb{S}_B\pmb{w}=\lambda\pmb{w}\) ,再将(19)式的 \(\pmb{S}_B\) 代入此时,得到:
这与(34)式雷同,只不过(40)中的 \(\lambda\) 是拉格朗日乘数,但形式一样,故可得:
与(29)同样的结果。
2.6 小结#
在以上讨论中,使用三种方法找到了 \(\pmb{w}\) 的方向,至此,事实上实现的是数据的降维(注意区别于 PCA),并没有实现对数据属于哪一个类别的“判别分析”——这一点非常重要,有的资料就此为止,未继续阐明如何判断所属类别。
当找到了 \(\pmb{w}\) 方向之后,假设有数据 \(\pmb{x}\) ,要判断属于哪一个类别,必须还要有阈值 \(w_0\) ,即:
当 \(\pmb{w}^\text{T}\pmb{x}\le-w_0\) 时,\(\pmb{x}\) 属于 \(C_1\) 类
否则,属于 \(C_2\) 类
而 \(w_0\) 是多少?这在费雪的线性判别分析中并未提及。所以需要进一步探讨。
下面要探讨 \(w_0\) 是多少,并进而实现对数据所述类别的判别分析。
3. 计算判别阈值#
如果要判别某个样本属于哪一类,必须计算出阈值 \(w_0\) ,求解方法有两种:
贝叶斯方法。此方法在另外一篇《线性判别分析》中详解
最小二乘法。此处演示此方法的求解过程
3.1 最小二乘法\(^{[6]}\)#
关于最小二乘法的详细讲解,请阅读参考资料 [2] 的有关章节,在其中对最小二乘法通过多个角度给予了理论和应用的介绍。
将两个类别的线性边界写作:
相应的最小平方误差函数:
其中,\(r_i\) 是样本数据的类别标签,即样本类别的真实值。若 \(i\in C_1\) ,则 \(r_i\) 为正例,否则为负例,不妨分别假设两个类别的标签分别是:
将(43)式分别对 \(w_0\) 和 \(\pmb{w}\) 求导:
令(44)式为零,即:
所以:
其中:
\(\frac{1}{n}\sum\limits_{i=1}^n\pmb{x}_i\) 是样本平均值(向量),记作 \(\pmb{m}\) ;
前述(43-2)式 \(r_{i,i\in C_1}=\frac{n}{n_1},r_{i,i\in C_2}=-\frac{n}{n_2}\) ,则 \(\frac{1}{n}\sum\limits_{i=1}^nr_i=\frac{1}{n}(n_1\frac{n}{n_1}-n_2\frac{n}{n_2})=0\) 。
所以,(47)最终得:
而对于 \(\pmb{w}\) ,在前述最优化求解中,已经得到:\(\pmb{w}\propto\pmb{S}^{-1}_W(\pmb{m}_2-\pmb{m}_1)\) ,(如(41)式),又因为 \(\pmb{w}\) 的表示的是方向(单位向量),或者说直线的长度不影响边界,故可直接令:
于是,可以用:
作为判别标准。
3.2 检验#
若 \(\pmb{x}=\pmb{m}_1\) ,很显然,此样本属于 \(C_1\) 类,利用(50)式对此结论进行检验:
由(18)式知:\(\pmb{S}_W^{\text{T}}=\pmb{S}_W\Longrightarrow(\pmb{S}_W^{-1})^\text{T}=\pmb{S}_W^{-1}\)
\(\pmb{m}=\frac{1}{n}\sum\limits_{i=1}^n\pmb{x}_i=\frac{1}{n}(n_1\pmb{m}_1+n_2\pmb{m}_2)\)
于是,(51)式继续计算如下:
其中的 \(\pmb{S}_W^{-1}\) (半)正定。
检验成功。
3.3 用最小二乘法计算 \(\pmb{w}\)#
用最小二乘法能够计算出 \(\pmb{w}_0\) ,也可以计算 \(\pmb{w}\) 。前面已经计算过了 \(\pmb{w}\) 的方向,这里再用最小二乘法计算,作为对此方法的深入理解。
在(45)式中,得到了 \(\frac{\partial E}{\partial\pmb{w}}\) ,令它等于零,则可以计算 \(\pmb{w}\) ,但是步骤比较繁琐,以下仅供参考。
由(17)式可得:
所以:
令(45)式的 \(\frac{\partial E}{\partial\pmb{w}}=0\) ,即:
下面对上式等号左右两边分别计算:
因为 \(\left(-\frac{n_1n_2}{n}(\pmb{m}_2-\pmb{m}_1)(\pmb{m}_2-\pmb{m}_1)^\text{T}\pmb{w}-n\right)\) 是数量(标量),所以:
4. 多类别的判别分析\(^{[6]}\)#
前面讨论的问题是基于 2.1 节中数据假设,即二分类问题,如果将上述两个类别下的类内散度和类间散度矩阵推广到多类别,就可以实现多类别的判别分析。
4.1 多类别的类内散度矩阵#
(18)式定义了 \(x\) 空间两个类别的类内散度矩阵,将其定义方式可以直接推广到多类别的类内散度矩阵:
其中:
\(\pmb{S}_j=\sum\limits_{i\in C_j}(\pmb{x}_i-\pmb{m}_j)(\pmb{x}_i-\pmb{m}_j)^\text{T},\quad{j=1,2,\cdots,k}\) ,
且 \(\pmb{m}_j=\frac{1}{n_j}\sum\limits_{i\in C_j}\pmb{x}_i\quad{j=1,\cdots,k}\) ,共计有 \(k\) 个类别。
\(n=n_1+\cdots+n_k\) 表示总样本数等于每个类别样本数的和。
4.2 多类别的类间散度矩阵#
多类别的类间散度矩阵,不能由(19)式直接推广。
令 \(\pmb{m}\) 表示 \(x\) 空间的全体样本的平均数(向量),即: $\( \pmb{m}=\frac{1}{n}\sum\limits_{i=1}^n\pmb{x}_i=\frac{1}{n}\sum\limits_{j=1}^k\sum_{i\in C_j}\pmb{x}_i=\frac{1}{n}\sum\limits_{j=1}^k(n_j\pmb{m}_j)\tag{59} \)$
对于所有的样本,仿照样本(有偏)方差的定义,可以定义针对 \(X\) 空间的所有样本的 Total scatter matrix(参考资料 [1] 中称为“全局散度矩阵”。愚以为,由于此概念是针对当前数据集所有样本而言——依然是抽样所得,如果用“全局”一词,容易引起与“总体”的错误联系,其真正含义是:本数据集所有样本散度矩阵):
将(60)式进一步写成:
因为:
由(58)式可得:\(\sum\limits_{j=1}^k\sum\limits_{i\in C_j}(\pmb{x}_i-\pmb{m}_j)(\pmb{x}_i-\pmb{m}_j)^\text{T}=\pmb{S}_W\)
\(\sum\limits_{j=1}^k\sum\limits_{i\in C_j}(\pmb{m}_j-\pmb{m})(\pmb{m}_j-\pmb{m})^\text{T}=\sum\limits_{j=1}^kn_j(\pmb{m}_j-\pmb{m})(\pmb{m}_j-\pmb{m})^\text{T}\)
因为 \(\sum\limits_{i\in C_j}(\pmb{x}_i-\pmb{m}_j)=0\) (每个样本与平均数的差求和,结果为 0 ),故得: \(\sum\limits_{j=1}^k\sum\limits_{i\in C_j}(\pmb{x}_i-\pmb{m}_j)(\pmb{m}_j-\pmb{m})^\text{T}=\sum\limits_{j=1}^k(\pmb{m}_j-\pmb{m})\sum\limits_{i\in C_j}(\pmb{x}_i-\pmb{m}_j)^\text{T}=0\)
所以,(61)式为:
令:
即为多类别的类间散度矩阵。
对于(63)式,如果 \(k=2\) ,即为二类别下的类间散度矩阵:
(64)式最终得到的二类别下的类间散度矩阵和(19)式相比,多了系数 \(\frac{n_1n_2}{n}\) ,因为它是常数,不会影响对 \(J(\pmb{w})\) 最大化求解。
4.3 多类别样本下的费雪准则#
假设由 \(q\) 个单位向量 \(\pmb{w}_1,\cdots,\pmb{w}_q\) 作为 \(X\) 空间样本数据 \(\pmb{x}\in\mathbb{R}^d\) 投影的超平面(直线)方向,得到:
写成矩阵形式:
其中 \(\pmb{W}=\begin{bmatrix}\pmb{w}_1&\cdots&\pmb{w}_q\end{bmatrix}\) 是 \(d\times q\) 矩阵。
由此,得到了 \(X\) 空间的样本 \(\pmb{x}_1,\cdots,\pmb{x}_n\) 投影到 \(\pmb{w}_l,(1\le l\le q)\) 上的投影,即得到 \(Y\) 空间的数据 \(\pmb{y}_i,(i=1,\cdots,n)\) :
仿照 \(X\) 空间计算平均值(向量)的方法,计算 \(Y\) 空间投影数据的平均值:
从而定义 \(Y\) 空间的类内散度矩阵和类间散度矩阵
将(67)(68)代入到(70),得到:
将(68)(69)带入到(71),得到:
由此,多类别下的费雪准则,其目标函数有两种表示方式:
第一种:用矩阵的迹表示
\[ J_1(\pmb{W})=\text{trace}\left(\hat{\pmb{S}}^{-1}_W\hat{\pmb{S}}_B\right)=\text{trace}\left((\pmb{W}^\text{T}\pmb{S}_W\pmb{W})^{-1}(\pmb{W}^\text{T}\pmb{S}_B\pmb{W})\right)\tag{74} \]第二种:用行列式表示
\[ J_2(\pmb{W})=\frac{|\hat{\pmb{S}}_B|}{|\hat{\pmb{S}}_W|}=\frac{|\pmb{W}^\text{T}\pmb{S}_B\pmb{W}|}{|\pmb{W}^\text{T}\pmb{S}_W\pmb{W}|}\tag{75} \]
不论以上哪种形式,最终均可得到如下最优化条件:
由上式得:\(\pmb{S}^{-1}_W\pmb{S}_B\pmb{w}_l=\lambda_l\pmb{w}_l\) 。参考(30)式之后的推导,\(\lambda_l\) 为广义特征值,\(\pmb{w}_l\) 是广义特征向量。以(74)式为例,可得如下结论(详细推导过程,请见参考资料 [7] 中的推导过程)
因特征值非负,故 \(q=\text{rank}(\hat{\pmb{S}}^{-1}_W\hat{\pmb{S}}_B)\) 。
又因为 \(\hat{\pmb{m}}\) 是 \(\hat{\pmb{m}}_1,\cdots,\hat{\pmb{m}}_k\) 的线性组合,故:
故 \(q\le k-1\) 。
给定包含 \(k\ge2\) 个类别的样本,多类别判别分析所能产生有效线性特征总数最多是 \(k-1\) ,即降维的最大特征数。
参考资料#
[1]. 周志华. 机器学习. 北京:清华大学出版社
[2]. 齐伟. 机器学习数学基础[M]. 北京:电子工业出版社
[3]. 拉格朗日乘数法
[4]. 广义特征值与极小极大原理。以下为此参考文献部分内容摘抄:
1、定义:设 \(\pmb{A}\) 、\(\pmb{B}\) 为 \(n\) 阶方阵,若存在数 \(\lambda\) ,使得方程 \(\pmb{Ax}=\lambda\pmb{Bx}\) 存在非零解,则称 \(\lambda\) 为 \(\pmb{A}\) 相对于 \(\pmb{B}\) 的广义特征值,\(\pmb{x}\) 为 \(\pmb{A}\) 相对于 \(\pmb{B}\) 的属于广义特征值 \(\lambda\) 的特征向量。
当 \(\pmb{B}=\pmb{I}\)(单位矩阵)时,广义特征值问题退化为标准特征值问题。
特征向量是非零的
广义特征值的求解
\((\pmb{A}-\lambda\pmb{B})\pmb{x}=\pmb{0}\) 或者 \(( \lambda\pmb{B}-\pmb{A})\pmb{x}=\pmb{0}\)
特征方程:\(\text{det}(\pmb{A}-\lambda\pmb{B})=0\)
求得 \(\lambda\) 后代回原方程 \(\pmb{Ax}=\lambda\pmb{Bx}\) 可求出 \(\pmb{x}\)
2、等价表述
\(\pmb{B}\) 正定,且可逆,即 \(\pmb{B}^{-1}\) 存在,则:\(\pmb{B}^{-1}\pmb{Ax}=\lambda\pmb{x}\) ,广义特征值问题化为了标准特征值问题。
3、广义瑞丽商
若 \(\pmb{A}\)、\(\pmb{B}\) 为 \(n\) 阶厄米矩阵(Hermitian matrix,或译为“艾米尔特矩阵”、“厄米特矩阵”等),且 \(\pmb{B}\) 正定,则:
\(R(\pmb{x})=\frac{\pmb{x}^\text{H}\pmb{Ax}}{\pmb{x}^\text{H}\pmb{Bx}},(\pmb{x}\ne0)\) 为 \(\pmb{A}\) 相对于 \(\pmb{B}\) 的瑞丽商。
[5]. 谢文睿,秦州. 机器学习公式详解. 北京:人民邮电出版社
[6]. 线代启示录:费雪的判别分析与线性判别分析
说明#
若读者发现本文中的错误或者其他有关问题,请到如下地址发帖讨论:
