转置矩阵
Contents
转置矩阵#
《机器学习数学基础》第 2 章 2.3.2 节介绍了转置矩阵的基本概念,并且在之后的有关问题探讨中,经常会用到转置矩阵。为了能深入理解转置矩阵,转载参考资料 [1] 中以线性变换角度理解转置矩阵的意义的有关内容,供读者参考。
矩阵 \(\pmb{A}\) 为 \(m\times n\) ,从线性变换的角度来看:\(\begin{split}\pmb{A}&:\mathbb{R}^n\to\mathbb{R}^m\\\pmb{A}^{\text{T}}&:\mathbb{R}^m\to\mathbb{R}^n\end{split}\)
如下图所示:
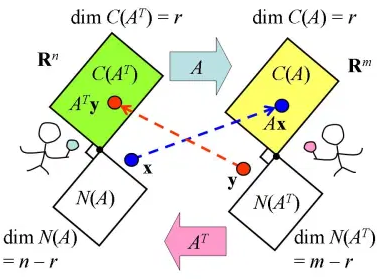
在“秩—零化度定理”中,对 \(\pmb{A}\) 和 \(\pmb{A}^{\rm{T}}\) 的列空间维数关系进行了阐述,请参考。
1. 转置矩阵的定义#
结合上图,设 \(\pmb{x},\pmb{A}^{\rm{T}}\pmb{y}\in\mathbb{R}^n;\pmb{y},\pmb{Ax}\in\mathbb{R}^m\) 。因为:
可得:\(\mathbb{R}^m\) 中的向量 \(\pmb{Ax}\) 与 \(\pmb{y}\) 的点积等于 \(\mathbb{R}^n\) 中的向量 \(\pmb{x}\) 与 \(\pmb{A}^{\rm{T}}\pmb{y}\) 的点积 \(^{[2]}\) 。
以上的性质,称为伴随(adjoint),利用这个性质定义转置矩阵:
设 \(m\times n\) 的实矩阵 \(\pmb{A}\) ,则转置矩阵 \(\pmb{A}^{\text{T}}\) 应满足:\((\pmb{Ax})^{\rm{T}}\pmb{y}=\pmb{x}^{\rm{T}}(\pmb{A}^{\rm{T}}\pmb{y})\) 。
参考文献#
[1]. 线代启示录:转置矩阵的意义
[2]. 关于内积和点积的详细内容,请参阅《机器学习数学基础》第1章1.4.2节。
