超平面
Contents
超平面#
在《机器学习数学基础》285页-286页,根据伯努利分布,推导出了 logistic 函数,并得到了286页的(5.3.16)式:
\[
\log\frac{P(C_1)|\pmb{x}}{1-P(C_1)|\pmb{x}}=\pmb{w}^{\text{T}}\pmb{x}+w_0\tag{5.3.16}
\]
将此式用于探讨线性判别分析,则有 \(\pmb{w}^\text{T}\pmb{x}+w_0=0\) ,在二维空间中,这表示的是直线,如果针对多维空间,则是超平面(hyperlane)。
1. 超平面的另一种定义方式#
1.1 代数定义#
对于三维空间中平面,如果推广到 \(\mathbb{R}^n\) 空间,即有线性方程组:
\[
\pmb{a}^{\text{T}}\pmb{x}=d\tag{1}
\]
的解所形成的集合(其中 \(\pmb{a}=\begin{bmatrix}a_1\\\vdots\\a_n\end{bmatrix},\pmb{x}=\begin{bmatrix}x_1\\\vdots\\x_n\end{bmatrix}\) ,\(d\) 是实数)就构成了超平面,其向量表达式可以写成:
\[
{H}=\{\pmb{x}\in\mathbb{R}^n|\pmb{a}^{\text{T}}\pmb{x}=d\}\tag{2}
\]
1.2 几何定义#
设 \(W\) 是 \(\mathbb{R}^n\) 的一个子空间,\(W\) 自原点平移 \(\pmb{q}\) 之后所得到的集合 \(S\) 称为仿射空间\(^{[1]}\),如下图所示。记作:
\[
S=W+\pmb{q}=\{\pmb{w}+\pmb{q} \mid \pmb{w} \in W\}\tag{3}
\]
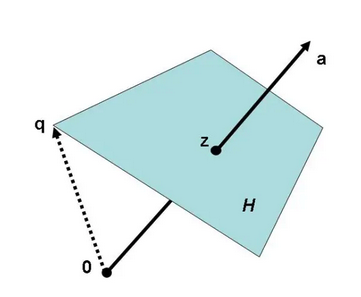
在 \(\mathbb{R}^n\) 中,超平面是一个维数等于 \(n-1\) 的仿射空间,或者说,除了 \(\mathbb{R}^n\) 本身,超平面是具有最大维数的仿射空间。
以上两个定义具有等价性。
参考资料#
[1]. 仿射变换[DB/OL]. https://lqlab.readthedocs.io/en/latest/math4ML/linearalgebra/affine.html
